7. SSHG analysis

Once the spectrum analysis for all the angles has been performed, see ref:polarisation_procedure_page, several observables can be extracted from the angle-dependent intensity data. Many possible analyses can be made depending on what you are looking for. We are detailing here the analysis commonly used at ILM.

See tutorial_SSHG for examples.

_images/alpaga_23.jpg

But, if you have developed your own code that extracts some observable from the intensity in function of the polarisation angle, please do not hesitate to contact us so that this code can be added in Alpaga!

The sshg_module of Alpaga is designed to extract susceptibility tensor coefficient \(\chi\) from polarisation resolved SSHG experiments on a isotropic and achirale interface. For that, we extract these coefficients by fitting our experimental data with the theoretical equations ( !!!REF!!!) :

\[\begin{split}I_{P}(\gamma) &\propto \lvert (a_2 \chi_{xxz} + a_3 \chi_{zxx} +a_4 \chi_{zzz}) cos^2(\gamma)+a_5 \chi_{zxx} sin^2(\gamma) \rvert ^2 \\ I_{S}(\gamma) &\propto \lvert a_1 \chi_{xxz} sin(2\gamma) \rvert ^2\end{split}\]

Where \(\gamma\) is the incoming polarization angle and {S, P} are the output polarization angles.

7.1. \(a_i\) coefficients

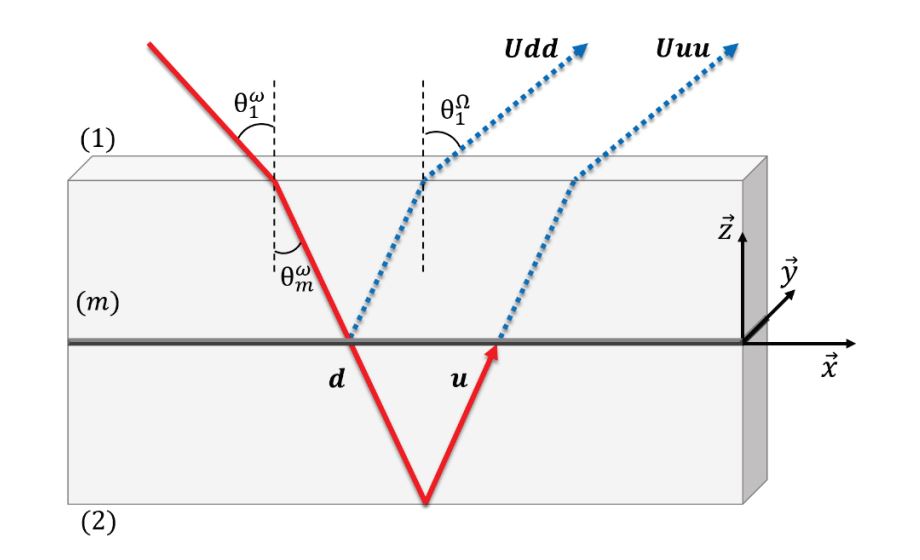
_images/three_layer_model.jpg

In order to extract the \(\chi\) coefficients, we first need a value of the ai coefficients. They are calculated from the three layer models [1], where an ‘interfacial’ layer produces the S-SHG signal. These ai coefficients contains the Fresnel transmission and reflexion coefficients at the different interfaces. In order to calculate them, we only need refractive indexes of the two bulk media at fundamental and harmonic frequencies, and the angle of incidence between the laser beam and the interface interface.

sshg_module.ai_coeff(angle1, n1, n2, N1, N2)[source]

From the experimental angle of incidence and the refractive index values of the materials (for both the fundamental and harmonic wavelengths), compute the ai coefficients and the reflection angle of the harmonic wave.

For details of the calculation, see Aurélie Bruyère’s thesis, pp. 70–81.

Parameters:

  • angle1 (float) – Experimental angle of incidence.

  • n1 (float) – Refractive index of medium 1 at the fundamental wavelength.

  • n2 (float) – Refractive index of medium 2 at the fundamental wavelength.

  • N1 (float) – Refractive index of medium 1 at the harmonic wavelength.

  • N2 (float) – Refractive index of medium 2 at the harmonic wavelength.

Returns:

ai – A list containing the computed ai coefficients and the reflection angle of the harmonic wave. The structure of the list is:

[a1, a2, a3, a4, a5, reflection_angle].

Return type:

list

7.2. Theoretical equation for SSHG intensities

Once the ai coefficients are calculated, one can calculate the intensity curves from some chi coefficients..

sshg_module.fit_polaS(x, chi_XXZ, ai)[source]

Defines the theoretical equation for S-polarized SHG intensity.

Parameters:

  • x (list) – The polarization angles of the fundamental wave, in degrees.

  • chi_XXZ (float) – The value of the chi_XXZ tensor element.

  • ai (list) – List of the ai coefficients, with the same structure as the output of sshg_module.ai_coeff.

Returns:

y – The S-polarized SHG intensity corresponding to the input angles.

Return type:

list

And :

sshg_module.fit_polaP(x, chi_XXZ, chi_ZXX, chi_ZZZ, ai)[source]

Defines the theoretical equation for P-polarized SHG intensity.

Parameters:

  • x (list) – The polarization angles of the fundamental wave, in degrees.

  • chi_XXZ (float) – The value of the chi_XXZ tensor element.

  • chi_ZXX (float) – The value of the chi_ZXX tensor element.

  • chi_ZZZ (float) – The value of the chi_ZZZ tensor element.

  • ai (list) – List of the ai coefficients, with the same structure as the output of sshg_module.ai_coeff.

Returns:

y – The P-polarized SHG intensity corresponding to the input angles.

Return type:

list

It also exists sshg_module.fit_pola45 function if you want to analyse some experiments with the outlet polarization angle fixed at 45°. These two functions are not the ones that make the fitting. They just describe how the theoritical equation evolve with the \(\gamma\) angle.

_images/alpaga_24.jpg

7.3. Fitting procedure to obtain Chi coefficients

The previous functions for \(a_i\) and theoretical intensities are combined in a single function which allow to extract \(\chi\) coefficients from experimental data. This function uses the datas and experimental parameters (such as medium refractive indexes and incidence angle of the fundamental beam) and, by fitting, returns the chi coefficients and ai.

It’s also important to note that with these equation there is two possible sets of coefficient that differs only for chi coefficient signs which are equivalent. We can distinguish the physical set by looking at the 45° polarisation.

sshg_module.analyse_polarization_SSHG(angle_incidence, n1_fonda, n2_fonda, n1_harmo, n2_harmo, L_polarisation_angle, L_intensity_S, L_intensity_P, XXZ=False)[source]

From the experimental angle of incidence, refractive indices of the materials for fundamental and harmonic wavelengths, polarization angles, and the SSHG Gaussian intensity, this function returns the ai coefficients and chi coefficients for an isotropic, achiral interface. Reference: Aurèlie Bruyere Thesis, pp. 70–81.

Parameters:

  • angle1 (float) – Experimental angle of incidence.

  • n1 (float) – Refractive index of medium 1 for the fundamental wavelength.

  • n2 (float) – Refractive index of medium 2 for the fundamental wavelength.

  • N1 (float) – Refractive index of medium 1 for the harmonic wavelength.

  • N2 (float) – Refractive index of medium 2 for the harmonic wavelength.

  • L_polarisation_angle (list) – The polarization angles of the fundamental in degrees.

  • L_intensity_S (list) – The SSHG intensity for S-polarized analyzer. The sizes of L_polarisation_angle and L_intensity_S must match.

  • L_intensity_P (list) – The SSHG intensity for P-polarized analyzer. The sizes of L_polarisation_angle and L_intensity_P must match.

  • XXZ (float or bool) – Optional parameter to fix the value of chi_XXZ. If, for example, the S polarization is flat, this avoids fitting the noise and recovering a non-physical value. By default, this is set to False, in which case chi_XXZ is extracted by fitting the S polarization.

Returns:

  • ai (list) – Contains the ai coefficients and the angle of the harmonic reflected wave. Structure: [a1,

    a2, a3, a4, a5, reflected angle of reflected wave]

  • list_chi (list) – Contains two mathematical solutions for the chi coefficients. Structure: [chi_XXZ,

    chi_ZXX, chi_ZZZ, chi_XXZset2, chi_ZXXset2, chi_ZZZset2]

A tuto is written to show how to use the module, how to plot the fit results and see the influence of the choice of the set of \(\chi\) coefficients over the 45° polarisation.

Release:

1.2

Date:

Aug 26, 2025