6.1. Overview: Optical Analysis¶

In $\texttt{FROG}$ , many properties can be computed from the structure given by the MD simulation: density, molecular orientation… None of these properties required the electronic degree of freedom one the dynamics given. The ‘’optical properties’’ defined in $\texttt{FROG}$ are the one which depend on the structure and the molecule electronic cloud.

Note

Here we do not say that these properties does not depend on the electronic degree of freedom since its impact the system’s dynamics. But once this dynamics is approach, calculation these property no longer involve electrons.

These properties are: the polarizaiblity, alpha and iota, and the first hyperpolarizability, beta and chi.

Note

The litteral name are used along with the grec notation: in the code the litteral name are used instead of the grec one for numerical obvious reason.

6.1.1. Scientific reminder:¶

Using a Taylor devellopment of a molecule dipole moment 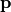$\bold{p}$ under an electrostatic field 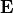$\bold{E}$ , the polarizability 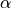$\alpha$ , the first hyperpolarizability 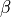$\beta$ (the first is dropped for simplicity) and the second hyperpolarizability 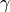$\gamma$ can be expressed as:

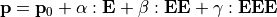
$\bold{p} = \bold{p}_0 + \alpha : \bold{E} + \beta : \bold{E} \bold{E} + \gamma : \bold{E} \bold{E} \bold{E}$

Where 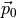$\vec{p}_0$ is the permament dipole moment of a molecule.

Note

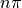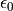The $n \pi$ and $\epsilon_0$ are dropped for simplicity.

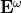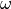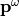Similary, when an electromagnetic field $\bold{E}^\omega$ at the frequency $\omega$ is shine on a molecule, it induces a dipole moment at similar frequency $\bold{p}^\omega$ :

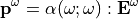
$\bold{p}^\omega = \alpha (\omega; \omega) : \bold{E}^\omega$

Or, if the electromagnetic field is large enough to higher harmonics. The first non-linear order is called the Sacond Harmonic Generation (SHG) and is the historical main target of $\texttt{FROG}$ . The induced dipole moment is at the double frequency 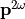$\bold{p}^{2 \omega}$ :

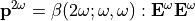
$\bold{p}^{2 \omega} = \beta (2 \omega; \omega, \omega): \bold{E}^\omega \bold{E}^\omega$

Where ‘:’ denotes tensorial products between 3x3 matrix or 3x3x3 matrix with 3D vector:

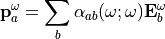
$\bold{p}^\omega_a = \sum_b \alpha_{ab} (\omega; \omega) \bold{E}^\omega_b$

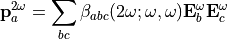
$\bold{p}^{2 \omega}_a = \sum_{bc} \beta_{abc} (2 \omega; \omega, \omega) \bold{E}^\omega_b \bold{E}^\omega_c$

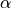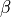The polarizability and hyperpolarizability tensor, $\alpha$ and $\beta$ , are properties of a molecule: they depend on (virtual) electronic transition moment and electronic energy gap. As long as the electromagentic field does not influence the states of the matter (individual or collective behaviors), these tensors describe the individual response of a molecule for linear and SHG proceses.

These tensors are space dependent, and are usually expressed in the molecular frame. In the molecular frame, the tensor used are 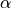$\alpha$ and $\beta$ :

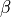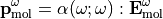
$\bold{p}^\omega_\text{mol} = \alpha (\omega; \omega) : \bold{E}^\omega_\text{mol}$

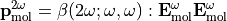
$\bold{p}^{2 \omega}_\text{mol} = \beta (2 \omega; \omega, \omega) : \bold{E}^\omega_\text{mol} \bold{E}^\omega_\text{mol}$

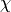In the laboratory frame, the tensor used are $\iota$ and $\chi$ , and depends on the molecule orientation:

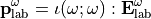
$\bold{p}^\omega_\text{lab} = \iota (\omega; \omega) : \bold{E}^\omega_\text{lab}$

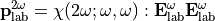
$\bold{p}^{2 \omega}_\text{lab} = \chi (2 \omega; \omega, \omega) : \bold{E}^\omega_\text{lab} \bold{E}^\omega_\text{lab}$

To go from one frame to another, the rotational matrix 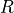$R$ is used:

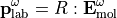
$\bold{p}^\omega_\text{lab} = R: \bold{E}^\omega_\text{mol}$

Using this rotational matrix, one can express the tensor in the molecular and laboratory frame, for instance:

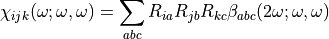
$\chi_{ijk} (\omega; \omega, \omega) = \sum_{abc} R_{ia} R_{jb} R_{kc} \beta_{abc} (2 \omega; \omega, \omega)$

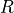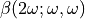In a real condensed phase, the response of the whole system is the response of every molecule within the laboratory frame. Thus, the optical response of the system is sensitive to the molecule orientation, $R$ , and the molecule individual optical property, $\beta (2 \omega; \omega, \omega)$ .

And here comes an important question: how to get the molecular orientation and the optical response in order to predict (non-linear) optical response of liquids.

Constant hyperpolarizability:

Let’s say that the hyperpolarizability tensor 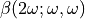$\beta (2 \omega; \omega, \omega)$ is the same for every molecule in the liquid. It make some sens: the MD force field you use every days to describes the net bulk water dynamics does not depend on the molecule. In this case, the optical response depends soleny on the molecule orientation. Therefore, to achieve this one has to compute only once the hyperpolarizability tensor, for instance in the vacuum phase.

Environment effects:

However, it has been shown that the electrostatic environment can affect the individual hyperpolarizability tensor 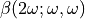$\beta (2 \omega; \omega, \omega)$ of molecule, for instance water. The charge position or the permanent dipole moment is mainly not very dependent on the environment because they depend on core electrons, which is not the case for optical response. Especially for non-linear reponse properties which are dramatically impacted by the most delocalised electrons and which are the more susceptible to the external electrostatic field.

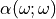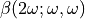In one hand, there is the need to average over the many configuration of the liquid phase to get properly converged resultats. In the other hand, each molecule optical properties may depends on its local environment, which involves to compute for every molecule its electronic degree of freedom to get the $\alpha (\omega; \omega)$ , $\beta (2 \omega; \omega, \omega)$ …

This is exactly the purpose of $\texttt{FROG}$ : computing the optical properties of molecule in liquid phase at electrostatic emmebbeded quantum level.

6.1.2. Available optical property:¶

Today, for every Molecule Type, $\texttt{FROG}$ can compute for every molecule the polarizability and the first hyperpolarizability. You may also compute the second hyperpolarizability with a bit of extra work – see the relative tutorial.

Note

The internal energy or dipole moment can be also easely computed by Frog. It is not yet implemented since the actual users do not look at these variables, but if you do please contact us.

Note

The effective field (or cavity field, or local felt electromagnetic field felt) is still under devellopment.

For the polarizability, use the diagram alpha and iota for the polarizability in the molecular and laboratory frame respectively.

For the hyperpolarizability, use the diagram beta and chi for the polarizability in the molecular and laboratory frame respectively.

For all these optical property, you can use the same value for all the molecule, or compute the individual value at the QM level. If you are using electrostatic emmebbeded QM calculation, you may be interested by the electrostatic field generated by the environment in the molecule vinicity. To keep track of it, use the diagram alpha.

6.1.3. Overview for the inputs:¶

For more complete exemples , see this first overview tutorial, this one for a more complexe electrostatic emmbedding scheme or this one for second hyperpolarizability calculation.

To perform optical analysis, you shall define the relative diagram first. For instance, to perform polarizability and hyperpolarizability calculation, first declare the diagrams:

L_diagram_analysis_to_perform = [
    ['electric_field', 'Averaged', [1, 200], [-10, 10], 'PE'],
    ['alpha', 'Averaged', [1, 200], [-25, 25]],
    ['iota', 'Averaged', [1, 200], [-25, 25]],
    ['beta', 'Averaged', [1, 200], [-35, 35]],
    ['chi', 'Averaged', [1, 200], [-35, 35]]
                              ]
moleculetype.read_diagram_input(GP, L_diagram_analysis_to_perform

Then, the optical properties inputs are given using the function moleculetype.read_optic_properties_input. This function has many options which are explained in different part of the documentation. Let’s focus on the major ones.

Since the polarizability and the hyperpolarizabilty have been required, $\texttt{FROG}$ needs to know how they should be computed: using a reference value or by a QM calculation. In this example, let’s say that the molecular polarizability is set to a reference value, and the hyperpolarizability should be computed:

L_alpha_ref = np.array([9.8, 0, 0], [0, 9.8, 0], [0, 0, 9.8]])
moleculetype.read_optic_properties_input(GP, alpha_calculation_style='Fixed for all', L_alpha_ref=L_alpha_ref, beta_calculation_style='QM', L_beta_ref=False)

The L_alpha_ref is used to defined the 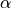$\alpha$ of every molecule of this MT, the iota is obtained by the product of this molecular polarizability with the molecular orientation – see here for more details.

Todo

Rajouter une page avec les equations de passage d ecrites?

Note

Every molecule of this MT will have the same molecular polarizability, alpha. Therefore, the diagram relative to the alpha are diracs.

The hyperpolarizability are computed by QM calculation. Therefore, a lot more information should be given.

First, which molecule of this MT should computed. To choose which molecule should be QM-computed, you can use 2 inputs: where_to_run_QM and selection_tool. ADD HYPERLINK to complete doc. If where_to_run_QM = [‘All’], then all the molecule of this MT may undergo QM calculation. Which is maybe what you want, but can lead to a lot of calculation very quickly. Moreover, in many cases, the optical response of some molecule are more interesting then other. For instance, for interfaces you may want to perform the calculation of the molecule only at the interface. For instance, using a plane discretization: where_to_run_QM = [‘Plane_xy’, 100, [50, 62, 63, 64, 65]], here 100 bins are used to discretize the z-laboratory axis. In this case, only molecule of this MT located at the bin 50, 62, 63, 64 or 65 in the z-laboratory axis are QM computed. The other do not contribute to the analysis.

Second, how the QM calculation are performed. $\texttt{FROG}$ use the software $\texttt{DALTON}$ to perform the QM calculation. To encode most of the information relative to the wat the QM calculation is performed, the object QMParameter is used ADD HYPERLINK. For this example, DFT framework is used with the Camb3lyp functional. For the basis set of the molecule, the d-aug-cc-pVTZ is used for all the atoms.

qmparameter = QMParameter()

qmparameter.theory_lv = 'DFT'
qmparameter.functional = 'Camb3lyp'
qmparameter.type_basis = 'Global basis'
qmparameter.global_basis_value = 'd-aug-cc-pVTZ'

Note

Today, only few of the available option of Dalton can be used. If you want to use other type of QM calculation, it may be very easy to implement in $\texttt{FROG}$ as it can be just lines to write in $\texttt{DALTON}$ input files.

With these parameters, $\texttt{DALTON}$ can compute the electronic states of a molecule of this MT, but to compute the hyperpolarizability, it needs the frequency. Indeed, a powerfull tool of $\texttt{DALTON}$ is to compute frequency-dependent polarizability and hyperpolarizabilities:

qmparameter.shg_response = [0.0, 0.05686] # should be given in a.u.,  0.05686 a.u. = 800nm, 0 a.u.= \infty nm

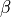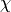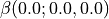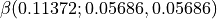In this case, the hyperpolarizabilities in the molecular and laboratory frame, $\beta$ and $\chi$ , are computed at 2 frequency: null and 0.05686 a.u. (which correspond to the infinite wave-length limite and 800~nm). In other words: $\beta(0.0; 0.0, 0.0)$ and $\beta( 0.11372; 0.05686, 0.05686)$ .

Note

The diagrams with beta and chi are duplicated for every frequency. In this case, there will be the diagram beta_0.0, beta_0.05686, chi_0.0 and chi_0.05686.

Finaly, the way the environement should affect each molecule are defined using the qmparameter.calculation_style attribute ADD LINK. For this example, the electrostatic field generated by the neighborhood of a molecule up to a distance of 10 angstrom are included.

qmparameter.calculation_style = 'PE'
qmparameter.pe_level = 0
qmparameter.max_pe_distance_neigh = 10

To have a look of the obtained neighborhood, a file can be generated for every configuration using:

qmparameter.write_xyz_environment = True

Moreover, since an electrostatic analysis with the option ‘PE’ has been set in the diagram initialization, the electrostatic field generated by this neighborhood is saved. The electric_field_PE diagram contains the distribution of this electrostatic field felt by each molecule.

6.1.4. Overview of the procedure:¶

Once the inputs read, $\texttt{FROG}$ goes to the first part where all the structural properties are computed for individual molecules. If some of the optical property do not need QM calculation, there are calculated as well. For instance for chi calculation within the constant beta approximation: all the molecule have the same beta and the chi depends only on the molecule orientation.

Todo

rajouter le concept du prepare_QM_run en tant que fausse analyse? Peut etre plus loin mais pas dans cette page pcq c est vraiment du detail

If QM calculation is needed, the input are prepared during this first part. For every molecule which should be computed, the Dalton input are written: 3 files are needed.

dalton.dal: The file containing the main choices of the QM calculation such as the functional to use or the frequency at which compute the polarizability or hyperpolarizability. These information are for the majority fixed for all the molecule of a MT and are defined in the QMParameter object.

molecule.mol: The file containing the atoms of the QM box. This can be one molecule or several. In this file, the coordinates are written within the laboratory frame. This file contains also the basis set used.

potential.pot: The file containing the eletrostatic neigborhood around the QM box. The ‘sites’ located in this file can contains point charge, dipole or quadrupole moment. This electrostatic emmebedding can also be made dynamics by adding polarizabilities.

Once these input file written for all the configurations (i.e. each molecules across all the MTs that should undergo a QM calculation for every time step), the list of all the QM calculation to performed is created.

In the second part, $\texttt{FROG}$ read this list of QM calculation to do, and create the submission script according to a template file. The generated files aims to submit thousands of calculation in a cluster. Then, $\texttt{FROG}$ stops and it is up to you to launch the main submission script which launch all the calculations to the cluster.

Warning

According to the first Frog author, submitting automatically jobs (and especially thousands) is a very bad behaviour and should always be done somehow manualy. Of course you may easily bypass this by runing automatically the main submission script after the end of $\texttt{FROG}$ execution. You have been warned.

Once all the calculation done, you may re-run $\texttt{FROG}$ with the option GP.pass_first_part = True ADD LINK. In this case, $\texttt{FROG}$ will go directly to the second part, and update the QM calculation to perform. To do so, it will try to read every $\texttt{DALTON}$ output files, all named dalton_molecule_potential.out, to check if the QM calculation have reached it final step.

Note

$\texttt{FROG}$ will not know if an error as been uncounter as long as the QM calculation reachs the last part. You may want to open by yourself several output file to check if everything is in order.

If $\texttt{FROG}$ finds the output file, and if it consider that the QM calculation ended, this configuration is considerated as complete. This procedure is repeated for every QM calculation to do. If some calculations are not done (no output file) or are not finished (they may have crashed), $\texttt{FROG}$ will recreate new set of subimission file to reperforme the QM calculation left to do. Until all the QM calculation are done, this loop of ‘second part -> new set of submission script -> QM run -> second part’ has to be repeated.

Note

In this case, you really want to look at the file in the directory of one of these ‘crashed’ calculation. You will find the output file as well as the error that may occurs. If sometimes it can be due to cluster related problems (like RAM memory crashes…), you may have a patological case which requires more attention.

If all the QM calculation have been performed, the second part lead to the first part of $\texttt{FROG}$ . In this part, the individual value of the optical properties which needed QM calculation are read from the $\texttt{DALTON}$ outputs. Then, the diagram are update with the molecule’s value and the whole $\texttt{FROG}$ procedure ends.